Welcome to a World of Menger Sponges
Content, images, & animation copyright © 1997-2026 Peter C. Miller.
Optimized Menger Sponge generation for 3d graphics:
At several points in my career, while testing 3d software and GPU hardware, I needed a basic polygonal model set which could easily grow in graphic content data density. The Menger Sponge fit the specification perfectly since each iteration allows for an arbitrarily defined level of complexity. I wrote several mel and Python scripts, each using different approaches to create Menger Sponges of different depths. Some are subtractive boolean in their approach, some are simply additive, some use basic replacement.
For those readers familiar with 3d technology, obviously the efficient way to go about rendering a Menger Sponge is via a custom shader, not with actual polygonal geometry. So to those interested in pure rendering fps rates and practical optimizations, the geometric approach described below may seem quite unnecessary or even counter productive. So I clarify here that my target realm is not efficiency, but testing and verifying the power of workstations, and in particular the capabilities of graphics cards. If "stressing the system to find the practical limits" is the goal, then this linearly-driven, geometry-based approach is (and has been) quite effective.
That said, I did not want inefficiency for inefficiencies sake. One problem I specifically wanted to address was that a casually formed Menger Sponge can commonly have unnecessary internal surfaces defined, which can seriously over-tax the target rendering engine, be that a graphics card or a software renderer. I also wanted to avoid duplicated polygonal vertices, which happily most 3d applications have efficient tools for removing.
The snapshots below describe this problem.
Menger Sponge level 1:
The same Menger Sponge in X-ray display:
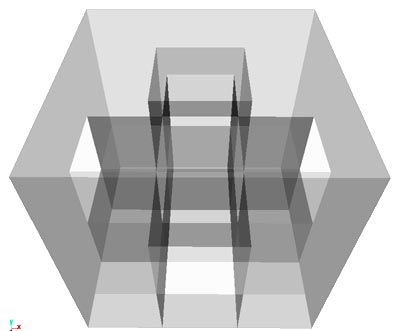
Same sponge, with unneeded internal surfaces displayed in
orange:
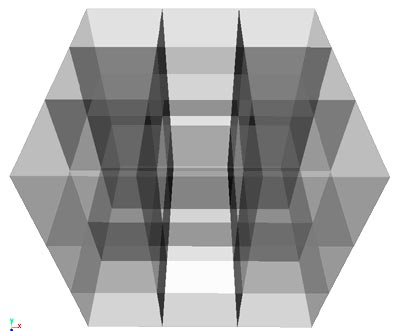
And a clean Menger Sponge, with no unneeded surfaces. In the example
below, only 24 surfaces were removed, not much improvement... but that
doesn't last long:
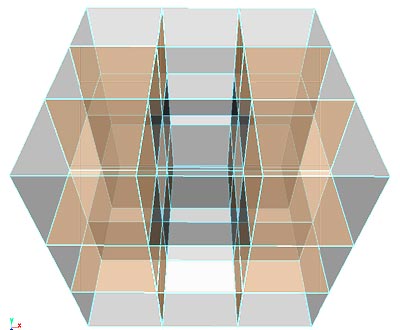
Same again - only this time a level 2 with unnecessary duped surfaces,
with 2,400 faces total:
And a "clean" Menger Sponge of level 2 as well, consisting of a more
tidy 1,056 faces:
You can see the removal of unnecessary surfaces can add up. And this is only level 2; for a level 3 there are 18,048 faces if it is built clean, while a 'lazy' level 3 Menger Sponge will have 48,000 faces. My scripts can build clean or lazy to any arbitrary level, with a maximum ceiling being of the amount of memory Maya consumes for the geometry data. Clearly this maximum level is higher if the scripts are run with the more recent 64 bit versions of Maya. Obviously as well building clean takes a bit more processing time.
Another point of clarification - these "clean" Menger Sponges are "pure" in the sense that no surfaces exist that are hidden, and every surface that exists is necessary and could be viewed from "outside" the sponge if a camera could be placed appropriately within the sponge. In other words, these clean/pure Menger Sponges could be filled with water from the inside, they would not leak.
So these Menger Sponges have neither unnecessary internal surfaces or duplicated vertices. So far I've used these scripts to make clean Menger Sponges level 1-6 in Maya. Keep in mind a level 6+ Menger Sponge really needs 64 bit memory space in Maya. (Memory consumption is ~200-250 bytes per vertex)
My Menger Sponge generation scripts were helpful for stress testing both software and hardware at Alias|wavefront (Owner of Maya before Autodesk), DreamWorks Animation), (for their 'Premo' animation tool's interactive display and 'Moonray' renderer,) and some personal projects, some of which are shown below.
Here's a simple animation of Menger Sponges (Menger Cubes) level 0-5:
Content, images, & animation copyright © 1997-2026 Peter C. Miller.
Some Hi Res OGL Renderings of Level 5
Lower corner view:
The above image is a hardware display capture with Maya's "Display Edges" turned on. It's cool to clearly see and count the open holes that are present from the largest to the smallest down to level 5.
"Street view":
This image positions the viewer slightly above the lowest level, looking
upward through the Menger Cube as though it were a monumental architectural
structure. At building scale, the Menger sponge offers a compelling case
study in fractal architecture and hierarchical porous systems—an approach
that contrasts sharply with the slender “Pencil Towers” that have
proliferated in Manhattan and other global financial districts. While those
towers emphasize iconic verticality and maximum floor-plate efficiency
through minimal footprints, they often contend with significant engineering
challenges: wind-induced dynamic response, cumulative construction
tolerances over extreme heights, and concentrated structural loads. A Menger
sponge building, by contrast, embodies a radically different paradigm of
distributed mass, volumetric porosity, and self-similar scaling.
The iterative removal of cubic volumes creates a lightweight yet highly
redundant lattice in which loads are transferred across a network of
smaller-scale elements at every level of iteration. This hierarchical
organization echoes principles observed in natural porous structures—most
notably the diagonally reinforced lattice skeleton of the glass sponge
Euplectella aspergillum (Venus’ flower basket), whose crossed-diagonal
bracing has been shown to achieve superior buckling resistance and
strength-to-weight performance compared with conventional lattice designs.
(wikipedia.org)
(materialdistrict.com)
Applied at architectural scale, such porosity would inherently reduce
overall dead load while providing exceptional resilience against gravity,
seismic, and wind forces. The open framework also facilitates deep daylight
penetration, natural cross-ventilation, and the integration of planted “sky
courts” or vertical gardens within the voids—aligning with contemporary
goals of biophilic design and passive environmental performance.
A Native 3D Circulation Network
Perhaps the most transformative architectural opportunity lies in the
sponge’s intrinsic network of intersecting voids. At each iteration, the
Menger construction generates a continuous, orthogonal system of horizontal
corridors and vertical shafts that together form a fully three-dimensional
graph of movement paths. These channels could be engineered as a
multi-directional transportation infrastructure—essentially embedding a
city-scale transit network directly into the building’s structural logic.
Emerging ropeless elevator technologies, such as the MULTI system developed
by TK Elevator (formerly ThyssenKrupp), demonstrate that cable-free cabins
propelled by linear induction motors or magnetic levitation can travel
vertically, horizontally, and even along looping pathways within shared
shafts.
(propmodo.com)
(dezeen.com)
A Menger sponge geometry would provide a ready-made lattice of such shafts
at multiple scales: grand central atria and cross-tunnels at lower
iterations for high-capacity public transit loops, and finer-grained local
channels at higher iterations for personalized or autonomous pods.
Passengers could select direct or optimized routes through the
three-dimensional matrix, dramatically reducing wait times and eliminating
the vertical-then-horizontal bottlenecks of conventional skyscrapers.
Redundant pathways would enhance safety and resilience, while AI-coordinated
traffic management could optimize flow across the entire fractal network.
The result is true point-to-point mobility in three dimensions—something
that has long been a conceptual goal in visionary urbanism and arcology
proposals.
Aesthetically and experientially, the form would provoke immediate and
polarized responses. Its raw, recursive geometry might be likened to
science-fiction megastructures, yet this very honesty of construction offers
rich opportunities for material and façade innovation. Differentiated
treatment of the smallest cubic modules—alternating high-performance
glazing, perforated metal screens, precast concrete, or adaptive
solar-responsive surfaces—could modulate light, shadow, and thermal
performance while revealing the self-similar patterns at every scale. The
porosity itself becomes the primary architectural expression: a building
that is simultaneously massive and permeable, monumental and intricately
detailed.
Animation #1: "Miller's Menger Sponge"
Content, images, & animation copyright © 1997-2006 Peter C. Miller.
This above movie is an old concept rough animation of mine which depicts a series of Menger Sponges multiplying into each iteration of Menger Sponge depth rather than subdividing. To see the animation, click here or on the image above.
In the animation we watch, from the point of view of a person standing, a Menger Sponge growing from a 1 inch cube at level 0 to a 1,640 foot tall Menger Sponge at level 9.
This was achieved in a 32 bit memory space by simulating levels above level 4 with procedural texturing. This animation was inspired partially from the old "power of 10" movies. I plan to have a second version of this animation with object scale references (basketballs, chairs, cars, boats, 747's etc.) added to aid a sense of scale. This animation was made with Maya and several mel scripts driving the animation procedurally.
Animation #2: "Planet Menger"
Here is a short movie of Menger Sponges floating on a lonely planet filled with
terrifying scale conceptualizations:
Content, images, & animation copyright © 1997-2006 Peter C. Miller.
